Galois Theory (almost done)
Before the lecture
Motivation
My motivation was to understand why there is no solution in radicals to general polynomial equations of degree five or higher with arbitrary coefficients (Abel-Ruffini theorem).
I knew the fact but never had a chance to learn it. But I was so curious about it these days, and decided to check.
About learning material
YouTube video “Visual Group Theory - Lecture 6” was easy to understand.
You can find the slides of the lecture here.
Supplements
These themes are not covered in the video, but they are good to know.
- Kelin four group
- Hasse diagrams
- Fundamental theorem of algebra (complex numbers are algebraically closed.)
- Any plynomial with complex coefficients, having degree $d$, has at least one complex root.(Gauss)
How did I follow the video
I listened 6.1 - 6.3 at the first day.
Abel-Ruffini theorem is revealed at 6.6. Galois proved it with geometry. This is why the Galois is famous.
About the video
The videos are super educational, but he omitted some proof of theorem. We need to refer other materials to construct full logic toward the Abel-Ruffini theorem.
Definition of a field
- Two group structures are implemented. Both of the structures are abelian groups (addition on $F$ and multiplication on $F\setminus\{0\}$ ).
- The distributive law holds. $a(b+c) = ab + ac$.
- Examples: $\mathbb{Q}$, $\mathbb{R}$, $\mathbb{C}$, $\mathbb{Z}_{p}$ ($p$ is prime).
Definition of field extension
- If $F$ and $E$ are fields with $F$ in $E$, $E$ is an extension of $F$.
- examples: $\mathbb{R}$ in $\mathbb{C}$, $\mathbb{Q}$ in $\mathbb{R}$
- Both sets have the same addition and multiplication.
Field extension example 1
Think about the smallest extension field $F$ of $\mathbb{Q}$ that contains $\sqrt{2}$. It is called “$\mathbb{Q}$ adjoin $\sqrt{2}$”.
$$ F = \{a+b\sqrt{2} | a,b \in \mathbb{Q}\} $$
Field extension example 2
Think about the smallest extension field $F$ of $\mathbb{Q}$ that contains $i$. remarking as $\mathbb{Q}(i)$.
Splitting field
- $\mathbb{Q}(\sqrt{2})$ contains all of the roots of $f(x)=x^2-2$, so $\mathbb{Q}(\sqrt{2})$ is called splitting field of $f(x)$.
- The name splitting comes from that the elements of $\mathbb{Q}(\sqrt{2})$ split $f(x)$ into $(x+\sqrt{2})(x-\sqrt{2})$.
- Using large field, we can split the equation.
- Note that $\mathbb{Q}(\sqrt{2})$ is the smallest extension to split $f(x)$.
Basis of extension
- We can think $\mathbb{Q}(\sqrt{2}, i)$ as a vector space whose basis is $1$, $\sqrt{2}$, $i$, and $\sqrt{2}i$.
- All elements of $\mathbb{Q}(\sqrt{2}, i)$ can be represented as $a+b\sqrt{2}+ci+d\sqrt{2}i$, where $a,b,c,d \in \mathbb{Q}$.
Spoiler(?)
Snipping from the slide.
The numbers on the edge is the degree of polynomial whose roots need to adjoin.
Field automorphism
- $\phi: F \rightarrow F$ for field $F$.
- $\phi$ is a bijection.
- $\phi(a+b) = \phi(a) + \phi(b)$ and $\phi(ab) = \phi(a)\phi(b)$. In other words, $\phi$ preserves the group structures.
- Example: for $\mathbb{Q}(\sqrt{2})$, $\phi: a+b\sqrt{2} \rightarrow a-b\sqrt{2}$ is a field automorphism.
Automorphism and rational number
Proposition:
If $\phi$ is an automorphism of an extension field $F$ of $\mathbb{Q}$, then $\phi(q)=q$ for all $q\in\mathbb{Q}$.
A proof overview (in the slide):
- First, proof $\phi(1)=1$,
- Extend using structure preserving properties. For example, $\phi(2)=\phi(1+1)=\phi(1)+\phi(1)=2$
Galois group
Let $F$ be an extension field of $\mathbb{Q}$. The Galois group of $F$ is the group of automorphisms of $F$, denoted $\mathrm{Gal}(F)$.
Galois group example 1
$\mathrm{Gal}(\mathbb{Q}(\sqrt{2})) \cong C_2$.
$\cong$ is read “isomorphic to”, and the $C$ stands for Cyclic group. The automorphism just changes the sign of $\sqrt{2}$.
Galois group example 2
$\mathrm{Gal}(\mathbb{Q}(\sqrt{2}, i)) \cong V_4$.
$V_4$ is Klein’s four group. The automorphism changes the sign of $\sqrt{2}$ or $i$, or both of them.
Mysterious connection between “subfields of $F$” and “subgroups of $\mathrm{Gal}(F)$”.
Snipping from the slide. Analogy of field extention and dihedral group $D_3$
$\left(\mathrm{where\ }\zeta = \frac{-1+\sqrt{3}i}{2}\right)$.
The numbers on the edges are the number of cosets.
Reminder: coset, right coset and left coset, subgroup.
Algebraic numbers
A polynomial is a function:
$$ f(x) = a_nx^n + a_{n-1}x^{n-1} + \cdots + a_2x^2 + a_1x + a_0 $$
Let $F[x]$ denote the set of polynomials with coefficients in $F$, and call this “the set of polynomials over $F$.
Definition (from nLab): An algebraic number is a root of a polynomial with integer coefficients $\mathbb{Z}[x]$ (or, equivalently, with rational coeffients $\mathbb{Q}[x]$. It’s not obvious).
A number that is not algebraic over $\mathbb{Q}$ (e.g., $\pi$,$e$) is called transcendental.
- Question: Can all algebraic numbers be expressed using radicals?
- Answer from Galois: No
Good picture from a math magazine:
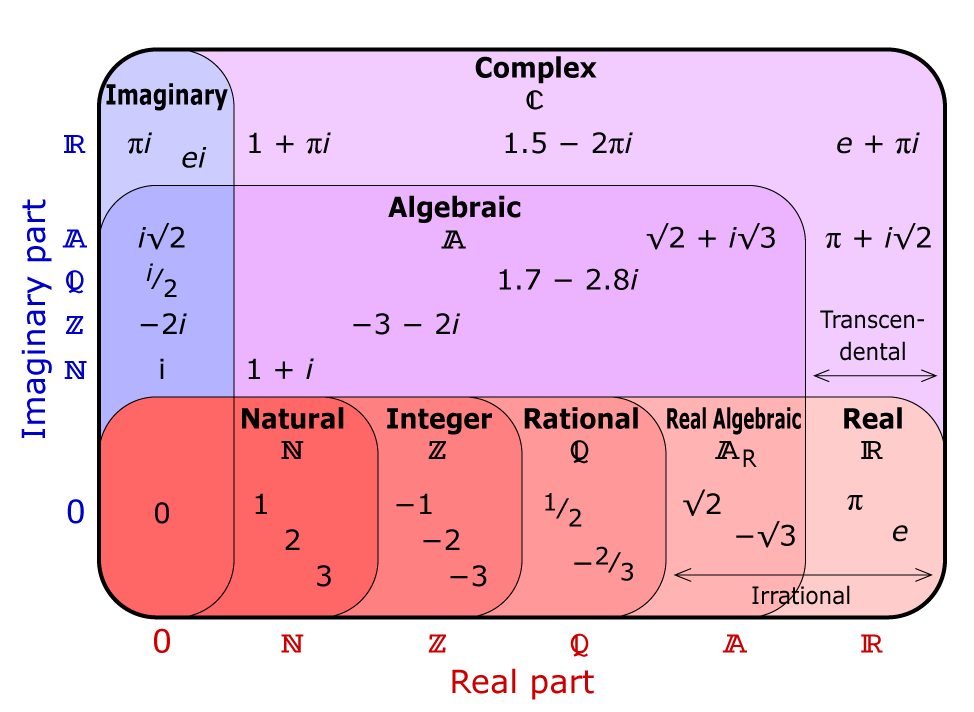
Algebraically closed field
(Wikipedia) A field $F$ is algebraically closed if every non-constant polynomial in $F[x]$ (the univariate polynomial ring with coefficients in $F$) has a root in $F$.
Example: Fundamental theorem of algebra
The field $\mathbb{C}$ is algebraically closed.
Here is very good conceptional proof of the theorem.
https://youtu.be/shEk8sz1oOw?t=572
Irreducibility of a polynomial
(From Wolfram MathWorld) A polynomial is said to be irreducible if it cannot be factored into nontrivial polynomials over the same field.
Irreducible is kind of unsplittable.
Eisenstein’s criterion
https://en.wikipedia.org/wiki/Eisenstein's_criterion
The criterion is a sufficient condition for a polynomial with integer coefficients to be irreducible over the rational numbers
Degree of a field extension
If $F$ and $E$ are fields and $F \subseteq E$, then the degree of the extension, denoted $[E : F]$, is the dimension of $E$ as a vector space over $F$.
For example, $[\mathbb{Q}(i, \sqrt{2}) : \mathbb{Q}] = 4$
Minimal polynomials
Let $r \notin F$ be algebraic. The minimal polynomial of $r$ over $F$ is the irreducible polynomial in $F[x]$ of which $r$ is a root. It is unique up to scalar multiplication.
Degree theorem
The degree of the extension $\mathbb{Q}(r)$ is the degree of the minimal polynomial of $r$.
This is non-trivial. I need to find proof.
Splitting field
Let $f \in \mathbb{Z}[x]$ be a polynomial, with roots $r_1,\cdots,r_n$. The splitting field of $f$ is the field $\mathbb{Q}(r_1,\cdots,r_n)$.
Galois group of a polynomial
The Galois group of a polynomial $f(x)$, denoted $\mathrm{Gal}(f(x))$ is the Galois group of its splitting field.
Tower low
For any chain of field extensions, $F \subset E \subset K$, $$ [K : F] = [K : E][E : F]. $$
Primitive elements
If $F$ is an extension of $\mathbb{Q}$ with $[F:\mathbb{Q}] < \infty$ then $F$ has a primitive element: some $\alpha\notin\mathbb{Q}$ for which $F=\mathbb{Q}(\alpha)$. The proof was skipped :)
Galois group of a polynomial and roots of the polynomial
Let $K$ be a field and $F$ be an extension field of $K$. Let $f(x)\in K[x]$. Then every automorphism in $\mathrm{Gal}(F/K)$ permutes the roots of $f(x)$ in $F$. ($F/K$ just denotes $F$ as an extension field of $K$.)
Easy proof) http://mathonline.wikidot.com/automorphisms-in-the-galois-group-of-f-x-over-k-permute-the
Hense, if the degree of $f \in \mathbb{Z}[x]$ is $n$, then the Galois group of $f$ is a subgroup of $S_n$. At this point, Galois theory and gerometry are connected with each other, and here is the fundamental about the proof Abel-Ruffini theorem.
Quick review: isomorphism and automorphism
Quickly referred here.
- “Automorphism” is used in various field (category) of math.
- “Isomorphism” is an automorphism in Group theory.
“One orbit theorem”
A tricky part of the lecture. I tried to imagine map $\phi:\mathbb{C}\rightarrow\mathbb{C}$
- Suppose an irreducable polynomial $f(x)$ over $\mathbb{Q}$.
- This implicit the existence of an extension field $F$ over $\mathbb{Q}$.
- Suppose roots of the polynomial is $r_1$ and $r_2$.
- An element of the Galois group of $f(x)$ permutes $r_1$ and $r_2$.
- It is not obvious, but there is an isomorphism $\phi:\mathbb{Q}(r_1)\rightarrow\mathbb{Q}(r_2)$ that fixes $\mathbb{Q}$ and with $\phi(r_1)=r_2$.
- We know, “an element Galois group permutes the root”, but we didn’t know the existence of the permutation for arbitrary roots. That’s why it’s not obvious.
I skipped the corollary.
From here, there are lots of non-obvious facts.
Normal field extensions
An extension field $E$ over $F$ is called a normal extension, which every irreducible polynomial over $F$ which has a root in $E$, splits into linear factors in $E$.
Normal extension theorem
The degree of a normal extension is the order of its Galois group.
And the order of the Galois group of polynomial $f(x)$ is the degree of the extension of its splitting field over $\mathbb{Q}$.
(There was no proof in the video. But this is no obvious.)
(need an example here)
Normal subgroup
Given a group $G$. A group $N\subseteq G$ is called a normal subgroup if $gN = Ng,\ \forall g\in G$.
As an equivalent definition: $\forall g\in G,\ gNg^{-1} = N$
Anothe requivalent definition: A subgroup ${\displaystyle N}$ of the group ${\displaystyle G}$ is normal in ${\displaystyle G}$ if and only if ${\displaystyle gng^{-1}\in N}$ for all ${\displaystyle g\in G}$ and ${\displaystyle n\in N}$.
We denote this as $N\triangleleft G$
Note that if $G$ is an abelian group then every subgroup $N$ of $G$ is normal.
Solvability
A group $G$ is called solvable if it has a chain of subgroups:
$$ \{e\} \triangleleft N_0 \triangleleft N_1 \cdots N_{k-1} \triangleleft N_k = G $$
s.t., each quotient $N_i/N_{i-1}$ is abelian.
No chain for $A_n$ where $n\geq5$
$S_n$ is about element swapping (permutation), and $A_n$ is about even number operation of the swapping. The official name is “Symmetric group” and “Alternating group”.
For $n\geq5$, the group $A_n$ is simple (whose only normal subgroups are the trivial group and the group itself) and non-abelian. So, the only chain is
$$ \{e\} \triangleleft A_n $$
, since $A_n$ is not solvable for $n\geq5$.
Annex. group theory
- Orbit, stabilizer: https://www.youtube.com/watch?v=AnJOjE8nVFY
- Cauchy’s theorem (wiki)
Quotient group
Based on a subgroup, original group could be categorized/devided.
For example, consider the group with addition modulo 6: $G = \{0, 1, 2, 3, 4, 5\}$. Consider the subgroup $N = \{0, 3\}$, which is normal because $G$ is abelian. Then the set of (left) cosets is of size three:
$$ G/N = \{ a+N : a \in G \} = \left\{ \{0, 3\},\ \{1, 4\},\ \{2, 5\} \right\} = \{ 0+N, 1+N, 2+N \}. $$