(Draft) Lattice-based crypto - introduction

Page content

During the Corona situation, I decided to learn something new, and it was lattice-based cryptography.

Intro to LWE from knapsack problem

From this slide

1D (modular) knapsack problem

Given $a_1, a_2,\cdots, a_n$ and $t$, $q$, where all variables are integers. Find $\{x_i\}_{i=1}^{n}\in\{0, 1\}^{n}$ s.t. , $$ t=\sum_{i=1}^{n}x_1a_i \bmod q. $$

Vector modular knapsack problem

Given $\pmb{a}_1, \pmb{a}_2,\cdots, \pmb{a}_n$ and $\pmb{t}$, $q$, where $\pmb{a},\pmb{t}\in\mathbb{Z}^{m\times1}$ and $q \in \mathbb{Z}$. Find $\pmb{x}=\{x_i\}_{i=1}^{n}\in\{0,1\}^{m\times1}$ s.t. , $$ \pmb{t}=\sum_{i=1}^{n}x_i\pmb{a}_i \bmod q. $$

We can extend the value of $x_i$ from $\{0, 1\}$ to $x_i\in\mathbb{Z}$ where $x_i\ll q$. This extension is $0-1$ kanpsack problem -> BKP (Bounded Knapsack Problem) -> UKP (Unbounded Knapsack Problem)

Vector modular knapsack problem in Matrix format

The equation can be expressed in Matrix form. Let $a_{ij}$ be “$i$-th element of the vector $\pmb{a}j$”. Hence $t_j = \displaystyle\sum{i=1}^{n} a_{ji}x_i\bmod q$, if we define a matrix $\pmb{A} = (\pmb{a}_1, \pmb{a}_2,\cdots,\pmb{a}_n)$, the vector knapsack problem can be expressed as follows:

Given $\pmb{A}\in\mathbb{Z}^{m\times n}$, $\pmb{t}\in\mathbb{Z}^{m\times1}$, and $q\in\mathbb{Z}$. Find $\pmb{x}\in\mathbb{Z}^{n\times1}$, s.t., $$ \pmb{A}\pmb{x}=\pmb{t}\bmod q. $$

How hard to solve the vector knapsack problem

  • If $n=m$, the problems can be solved easily by Gaussian elimination ($O(n^3)$).
  • If $n\neq m$, the unbounded knapsack problem (integer knapsack problem) is NP-complete.
  • Some are solavble in polynomial times. There is an algorithm (LLL lattice basis reduction) to get an approximate answer (or an exact answer sometimes) of this problem in polinomial time ($O(n^5m\log^3 a)$ where $A$ is the longest length of $\pmb{a}_i$ under the Euclidean norm), under som conditions (refer to Wikipedia).
  • So, in case of $n\neq m$, the time complecitiy is NP.

Example of LLL:

From knapsack to LWE

We can lead LWE from vector knapsack problem.Here is the step by step instructions. (I omitted all $\bmod q$.)

This is a visualized vector knapsack problem:

alt text
Vector knapsack problem.

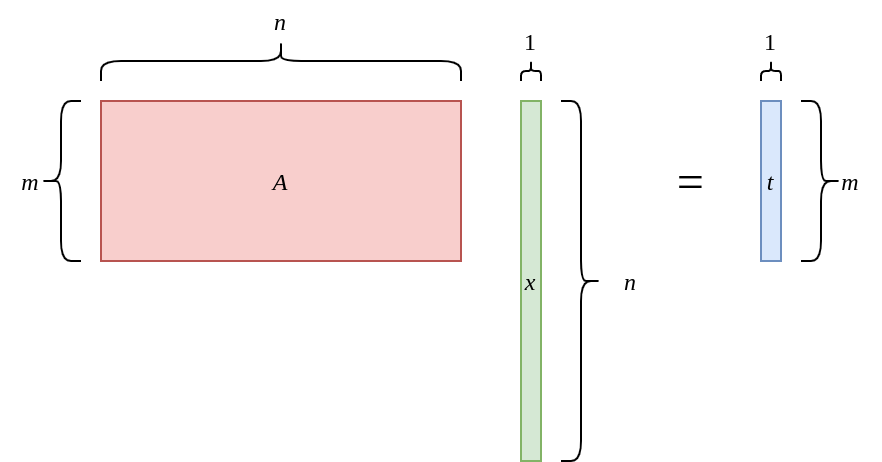
Split the Matrix $\pmb{A}$ as follows:

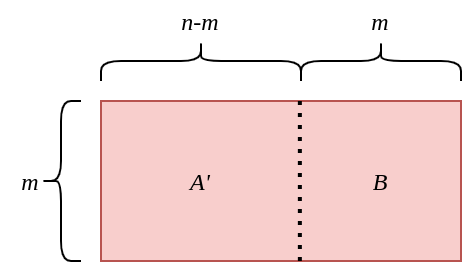
alt text
Split the matrix.

It can be written $\pmb{A}=\left[\pmb{A}’\ \pmb{B}\right]$.

Multiply $\pmb{B}^{-1}$ from left:

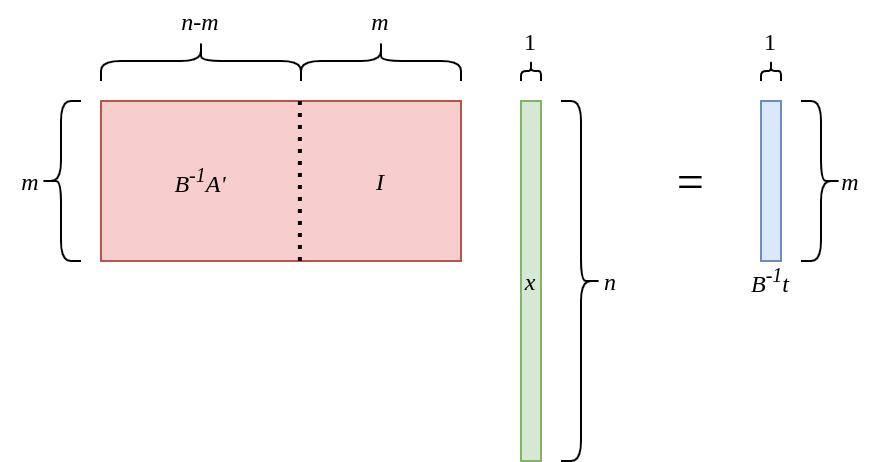
alt text
Multibly B^(-1).

Redefine $\pmb{B}^{-1}\pmb{A}$ as $\pmb{A}$, and $\pmb{B}^{-1}\pmb{t}$ as $\pmb{t}$:

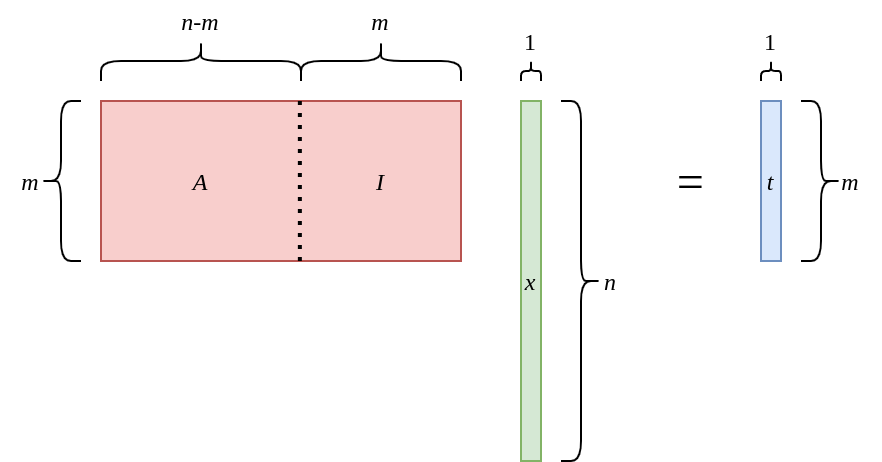
alt text
Redefine name.

Split the vector $\pmb{x}$ into $\pmb{x}=\ ^t[\pmb{s}\ \pmb{e}]$:

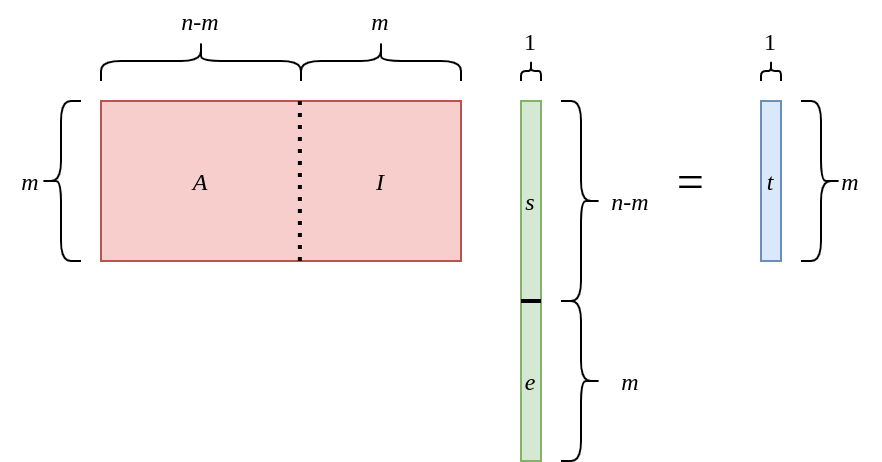
alt text
Split the vector x.

Split the multiplication:

alt text
Split the multiplication.

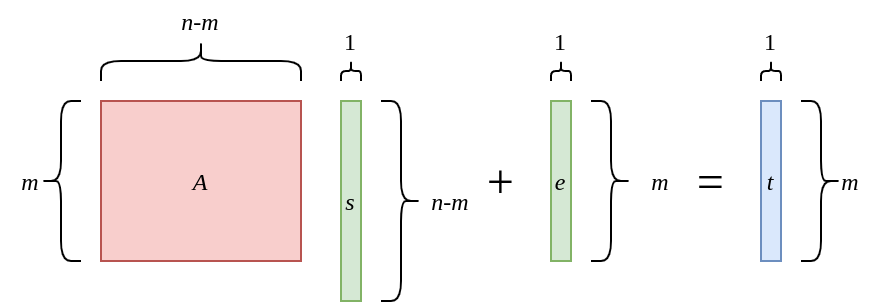
And finally, redfine $n-m$ as $n$:

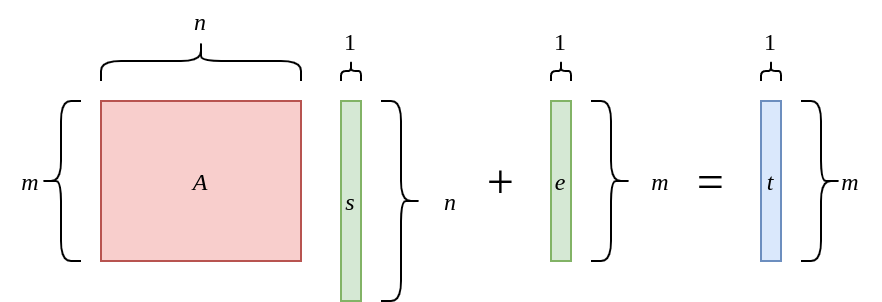
alt text
LWE.

This is the LWE (Learning With Errors).

Notes

The complexity of finding the inverse $\pmb{B}^{-1}$ is $\mathrm{P}$ (Gaussian elimination), but the complexity of “finding $\pmb{s}$ and $\pmb{e}$” is $\mathrm{NP}$, because the complexity of a vector knapsack problem is $\mathrm{NP}$.

LWE problem

The first definition of LWE appears in the famous paper from Regev.

You can find a free version from https://cims.nyu.edu/~regev/papers/qcrypto.pdf.

First, Regev introduced “learning from parity with error problem” as follows:

Let $\pmb{s}\in\mathbb{Z}^{n}_{2}$, $\pmb{a}_i\in\mathbb{Z}^{n}_{2}$, and $0 \leq \varepsilon\ll 1$.

Find $\pmb{s}$ from given pairs $\left(\pmb{a}_i, b_i\right)$, s.t., $$ \begin{align} \left<\pmb{s}\cdot\pmb{a}_1\right> &\approx_{\varepsilon} b_1 (\bmod 2) \\\ \left<\pmb{s}\cdot\pmb{a}_2\right> &\approx_{\varepsilon} b_2 (\bmod 2) \\\ &\ \cdot \\\ &\ \cdot \\\ &\ \cdot \end{align} $$ where $\approx_{\varepsilon}$ means “the result is wrong (error) with probability $\varepsilon$”.

This problem is one of the simplest 0-1 modular knapsack problem, if there is no error ($\varepsilon=0$).

From this problem we can extend:

  • $\bmod 2$ to $\bmod p$, where $p$ is a prime integer, and $p\leq\mathrm{poly}(n)$.
  • $\varepsilon$ to an error distribution function $\Psi$.

This extended problem is called $\mathrm{LWE}_{p,\Psi}$ problem.

Application to public key encryption

At the end of the paper from Regev, they propose how to apply this LWE problem into public key encryption.

Examples

https://www.esat.kuleuven.be/cosic/blog/introduction-to-lattice-based-cryptography-part-2-lwe-encryption/ <- contains some errors.

entities

  • Plain text: $m\in\mathbb{Z}$
  • Prime number $q$
  • Dimention $n$
  • $\pmb{A} \leftarrow \mathcal{U}(\mathbb{Z}_q^{n\times n})$
  • $\pmb{s} \leftarrow \mathbb{Z}_q^{n \times 1}$
  • $\pmb{e} \leftarrow \mathbb{Z}_q^{n \times 1}$
  • $\pmb{s}’ \leftarrow \mathbb{Z}_q^{n \times 1}$
  • $\pmb{e}’ \leftarrow \mathbb{Z}_q^{n \times 1}$
  • $e’’ \leftarrow \mathbb{Z}_q$

The $\pmb{s}$ is a secret key.

How to create public key: $$ \left( \pmb{A}, \pmb{b} = \pmb{A} \pmb{s} + \pmb{e} \bmod q \right) $$

How to encrypt $m$: $$ \pmb{b}’ = \pmb{A}^t \pmb{s}’ + \pmb{e}’ \bmod q \\\ v’ = \pmb{b}^t\pmb{s}’ + e’’ + \frac{q}{2} m \bmod q $$ I don’t innerproducts.

How to decrypt $v’$: $$ \Delta v := v’ – {\pmb{b}’}^t\pmb{s} \bmod q $$ It is $$ \begin{align*} \Delta v &= \left( \pmb{b}^t\pmb{s}’ + e’’ + \frac{q}{2}m \right) -\left({\pmb{s}’}^t \pmb{A}\pmb{s} + {\pmb{e}’}^t\pmb{s} \right) \bmod q \\\ &= \left( \pmb{s}^t\pmb{A}\pmb{s}’ + \pmb{e}^t\pmb{s} + e’’ + \frac{q}{2}m \right) -\left({\pmb{s}’}^t \pmb{A}\pmb{s} + {\pmb{e}’}^t\pmb{s} \right) \bmod q \end{align*} $$

real value example

  • Prime number: 17
  • Dimention: 3
  • $\pmb{A} = \left( \begin{array}{rrr} 3 & 11 & 12 \\\ 16 & 2 & 7 \\\ 9 & 0 & 1 \end{array} \right)$
  • $\pmb{s}^t = \left( \begin{array}{rrr} 1& 1& 0 \end{array}\right)$
  • $\pmb{e}^t = \left( \begin{array}{rrr} 0& 1& 0 \end{array}\right)$

https://www.slideserve.com/felcia/lattice-based-cryptography <- actual values.

LWE definition (Wiki) -> decisional LWE -> RLWE (polynomial) -> NTRU

From Regev’s paper

$\tilde{O}$: soft-O notation,

$$ f(n)\in {\tilde {O}}(g(n)) \iff \exists k:f(n)\in O(g(n)\log ^{k}g(n)) $$