Propositional and predicates logic
This is my note of the video https://youtu.be/V49i_LM8B0E. It’s not a full guide of propositional and predicates logic.
Mathmatics as a language of Physics
- Physics “casts” concepts about the real world into rigorous mathematical forms.
- Mathematics is just a language for the Physics. Physics interprets the meaning of mathematical statements.
- But to describe Mathematics, we need logic (especially, standard logic).
- Psycologically, an equivalent but a different form will help us to understand an interpretation.
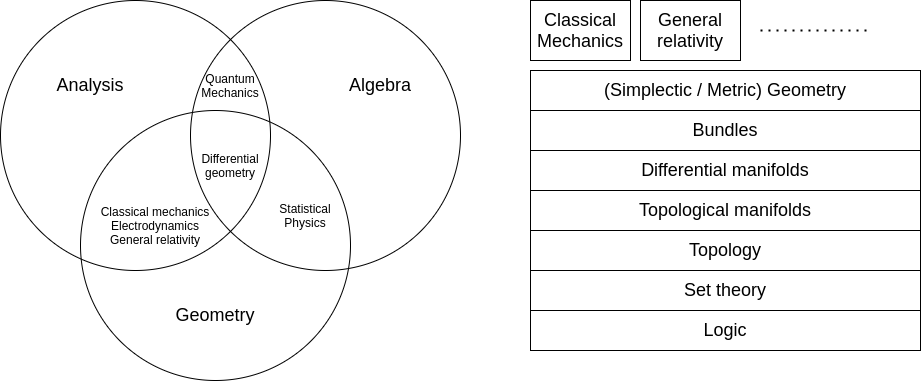
- Physical “spaces” are defined on a set. So the set theory would be a base.
- Axiomatic set theory is written in standard logic.
- To induce “contnuity”, we need topology on the set theory.
- One of interesting topology for Physics is topological manifolds.
Propositional Logkc
Quickly construct a propositional logic
A proposition $p$ is a variable that can take the values only “true ($t$)” or “false ($f$)”. It’s called law of excluded middle (principium tertii exclusi).
Propositional logic doesn’t decide, a proposition is true or false by itself. Propositional logic doesn’t convey meanings of propositions.
Logical operator
Unary operator: takes one proposition and makes a new proposition from it. There could be 4 unary operator as follows:
| $p$ | $\neg p$ | $^{id}p$ (Identity operator) | $^{\top}p$ (Tautology operator) | $^{\bot}p$ |
|---|---|---|---|---|
| $t$ | $f$ | $t$ | $t$ | $f$ |
| $f$ | $t$ | $f$ | $t$ | $f$ |
- defined the logic rules by tables, not deduction rules (another way).
- some logix cant be expressed in tables.
- Defining by deduction rules is more abstract, but in standard logic, it’s OK.
- didn’t use a terminology “map”.
- A tautology is a proposition (statement) that is always true.
Binary operater: takes two propositions and makes a new proposition from it. There are 16 binary operater, and here are some of binary operators:
| $p$ | $q$ | $p\land q$ | $p\lor q$ | $p\veebar p$ (Exclusive OR) | $p\Rightarrow q$ (Ex falso quodlibet) | $p\Leftrightarrow q$ | $p\uparrow q$ (NAND) |
|---|---|---|---|---|---|---|---|
| $t$ | $t$ | $t$ | $t$ | $f$ | $t$ | $t$ | $f$ |
| $t$ | $f$ | $f$ | $t$ | $t$ | $f$ | $f$ | $t$ |
| $f$ | $t$ | $f$ | $t$ | $t$ | $t$ | $f$ | $t$ |
| $f$ | $f$ | $f$ | $f$ | $f$ | $t$ | $t$ | $f$ |
- In the middle age, there was a discuss how to interpret “or” in the bible as OR or XOR. Frege and Wittgenstein answered “it’s just a table”.
- Ex falso quodlibet: can be interpreted as “from false, you can conclude anything and whole things are evaluted true.
- Once we interpert $\Rightarrow$ as “implies”.
- Keep in mind that logic just provide signes, and doesn’t provide interpretations by our natural language (but still similar to our natural languages. Refer to Wittgenstein).
Proof by contradiction
Theorem:
$$ (p\Rightarrow q) \Leftrightarrow \left(\left(\neg q\right)\Rightarrow\left(\neg p\right)\right) $$
It can be prooven by a table.
Corollary: We can prove assertions by the way of contradiction (proof by contradiction, reductio ad impossibile).
Remark 1: Agree on decreasing binding strength in the sequence:
$$ \neg , \land, \lor, \Rightarrow, \Leftrightarrow $$
Remark 2: All higher order operator (takes more than two propositions) can be constructed from a NAND (not and) operator.
Well-formed formula (WFF)
Not be mentioned in the video, but I just wanted to know the terminology. If I describe it here, the whole theme will diverge, so I’ll skip this time.
Predicate logic
A predicate is a proposition-valued function of some variable(s).
$$ \begin{aligned} P(x): &\text{ true or false, depend on }x \\\ Q(x,y): &\text{ true or false, depend on a combination of }x \text{and }y \end{aligned} $$
“How $P$ and $Q$ (actual predicates) are built” is not a topic of predicat logic. During defining set theory upon the logic, we think “what is the set of variable?” etc.
Construct predicates from proposition
Given a predicate $P$. We can construct a new following proposition:
$$ \forall x: P(x) $$
which is defined to be true if $P(x)$ is true independently of $x$. Usually, we just read it as “for all $x$, $P(x)$ is true” $\forall$ is called universal quantifier.
We used the word “independently”, without specifying a set.
We can define another proposition from the constructed proposition:
$$ \exists x: P(x) :\Leftrightarrow \neg\left(\forall x: \left(\neg P\left(x\right)\right)\right) $$
This proposition is read as “there exist an $x$ such that $P(x)$”. $\exists$ is called an existential quantifier.
Corollary (obtained by negation of the definition):
$$ \forall x: \neg P(x) \Leftrightarrow \neg\left(\exists x: P\left(x\right)\right) $$
Note that the order of quantifier matters:
$$ \forall x: \exists y: P(x,y) \text{ is generically different from } \exists y: \forall x: P(x,y) $$
Axiomatic systems & theory of proofs
Note that this is one of proof system.
Axioms
An axiomatic system is a finite sequence of propositions $a_1, a_2, \cdots , a_N$, which are called axioms of the system.
What is “finite”? What is $1$, and $N$ without set theory? Schuller mentioned that some logician call thoes number as pre-mathmatical number, used in “Barvarian pubs"🤣 We can write it as $a’, a’’, a’’’, \cdots$ instead. As far as I googled, pre-intuitionism would be what he mentioned. If we can construct the axioms of set theory only with the knowledge before this section, we can define natural numbers, but we can’t before defining what is an axiom.
Quotes from Wikipedia page:
For Poincaré, the definition of a mathematical entity is the construction of the entity itself and not an expression of an underlying essence or existence. This is to say that no mathematical object exists without human construction of it, both in mind and language.
Proof
A proof of a proposition $p$ within an axiomatic system $a_1, a_2, \cdots , a_N$ is a finite sequence of propositions $q_1, q_2, \cdots , q_M$ such that, $q_M\Leftrightarrow p$ and for any $1\leq j\leq M$ one of the following is satisfied:
- (Axiom): $q_j$ is a proposition from the list of axioms.
- (Tautology): $q_j$ is a tautology.
- (Modus ponens): $\exists m,n: 1\leq m,n<j \text{ and } (q_m\land q_n\Rightarrow q_j)$ is true.
If $p$ can be proven within an axiomatic system $a_1, a_2, \cdots, a_N$ , we write:
$$ a_1, a_2, \cdots, a_N \vdash p $$
We read $\vdash$ as “is provable, proves”.
Remarks 1: It’s easy to check a given proof is right or not (by computer), but logics doesn’t provide us how to find a proof efficiently.
Remarks 2: Axiomatic system for porpositional logic is an empty sequence. https://math.stackexchange.com/questions/2690830/showing-propositional-logic-is-consistent
Consistency
An axiomatic system $\Phi$ is consistent, if the axioms don’t lead to a logical contradiction. We usually write as $\operatorname{Con}\Phi$. An inconsistent one is written as $\operatorname{Inc}\Phi$.
Suppose an axiom $\Phi’$ is inconsistent. From definition, there is a proposition $s$, where $\Phi’\vdash s$ and $\Phi’\vdash \neg s$. In this case, you can prove any proposition $q$ by modus ponens ($s\land\neg s\Rightarrow q$).
An axiomatic system $a_1, a_2, \cdots, a_N$ is said to be (absolutely) consistent if there exists a proposition $q$ which cannot be proven from the axioms:
$$ \exists q: \neg(a_1, a_2, \cdots, a_N \vdash q) \\\ \exists q: a_1, a_2, \cdots, a_N \nvdash q $$
Refer to the Wikipedia page for more details.
Propositional logic is consistent
Simple proof:
Propositional logic can be regarded as an axiomatic system with empty axioms. That means, all propositions are “deduced” (proved) by tautologies and modus ponens. Hence, we can deduce only tautologies (true propositions) and there is no contracition. $\blacksquare$
Note that propositional logic is absolute consistent also, because it’s impossible to prove $q\land\neg q$.
Completeness
The whole theme will diverge if I describe more details, so I’ll skip this time.
Sideway: Gödel’s first incompleteness theorem
Any consistent axiomatic system within which a certain amount of elementary arithmetic can be carried out is incomplete; i.e., there are propositions of the system which can neither be proved nor disproved.
There is a Wikipedia page which sketches the proof: https://en.wikipedia.org/wiki/Proof_sketch_for_G%C3%B6del's_first_incompleteness_theorem
Reference
- Propositional logic by deduction rules?
- https://en.wikipedia.org/wiki/Axiomatic_system
- https://en.wikipedia.org/wiki/Vacuous_truth